La Cuadratura del Círculo
Se le llama "Cuadratura del Círculo" al problema matemático irresoluble según la "geometría", que consistente en hallar —con sólo regla y compás— un cuadrado que posea un área que sea igual al área de un círculo dado.
Como hemos mencionando anteriormente, la resolución de este problema trató de abordarse repetidas veces, aparentemente sin éxito, desde la antigüedad. Hablando en sentido figurado, se dice de algo que es la "Cuadratura del Círculo" cuando representa un problema muy difícil o imposible de resolver.


La Solución
Al igual que vimos en la "Cuadratura de la Circunferencia", la solución a este problema es relativamente sencilla desde cierta perspectiva y muy complicada desde otra, es sencillo dar con la solución numérica, pero es muy complicado dar con el detalle de como se genera dicha solución.
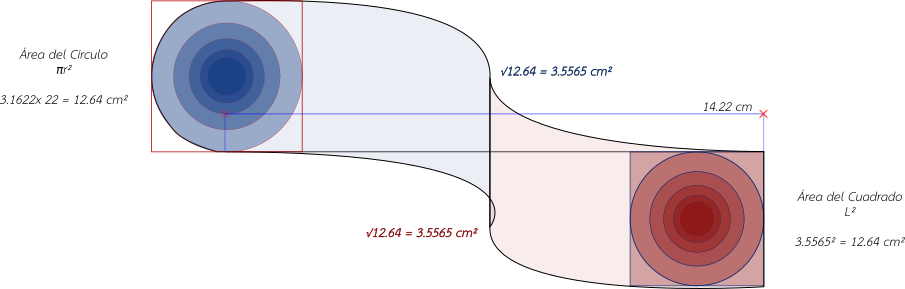
A diferencia de la "Cuadratura de la Circunferencia" en donde teníamos que usar el perímetro y la circunferencia, en la "Cuadratura del Círculo" necesitamos igualar el área del círculo con el área del cuadrado, lo que nos lleva a ir de una medida en centímetros (cm) a una solución en centímetros cuadrados (cm²), lo que es similar a la diferencia que hay entre una línea y un plano. En la "Cuadratura de la Circunferencia" teníamos que igualar el contorno tanto de la circunferencia como del cuadrilátero, pero aquí tenemos que igualar todo lo que se encuentra en el interior, es decir, todo el interior o área del círculo con el interior o área del cuadrado.
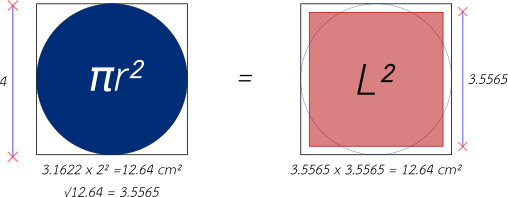
Calculamos el valor del área del círculo circunscrito en el cuadrado de lado 4, valor que nos da: A= ∏r² = 3.1622 x 2² = 12.6488 cm². Con esto presente, la solución numérica curiosamente sale de sacar la "raíz cuadrada" de ese mismo valor: √12.6488, lo que nos da 3.5565 cm, valor que representa el lado del cuadrado de 3.5565 x 3.5565 cm, cuya área nos proporciona el valor de 12.6488 cm², valor que representa un área equivalente a la del círculo circunscrito dentro del cuadrado de lado 4, equivalencia que nos permite dar con la solución de la "Cuadratura del Círculo", lo que nos permite encontrar la igualdad entre estas dos figuras "geométricas".
De esta manera, encontramos numéricamente un círculo y un cuadrado cuyas áreas son equivalentes. Ahora, como comenté, la solución numérica es sencilla, lo que es complicado es como encontrar el como se genera dicho cuadrado, utilizando solo "Regla y Compás", por lo que a continuación mostraremos una serie de métodos o posibles formas de poder encontrar dicho valor utilizando los números y la "geometría".