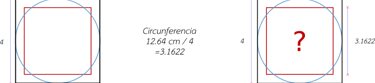The Quadrature of the Circumference
It is called as the "Quadrature of the Circumference" the mathematical problem according to "geometry", which consists in finding -with only ruler and compass- a quadrilateral that has a perimeter equal to the circumference of a given circle.
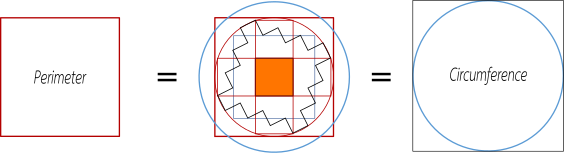
The Solution
The solution to this problem is relatively simple from a certain point of view and very complicated from another, it is easy to find the numerical solution, but it is very complicated to find the detail of how this solution is generated. We had mentioned that the "Quadrature of the Circumference" consists of finding a quadrilateral that has the same perimeter of a circle and we had also seen how it was, that in the "Fourth Progression" is the moment where the "numerical occurrence" occurs where the numerical value of the perimeter is equivalent to the numerical value of the area, associated to a quadrilateral of side 4 cm.
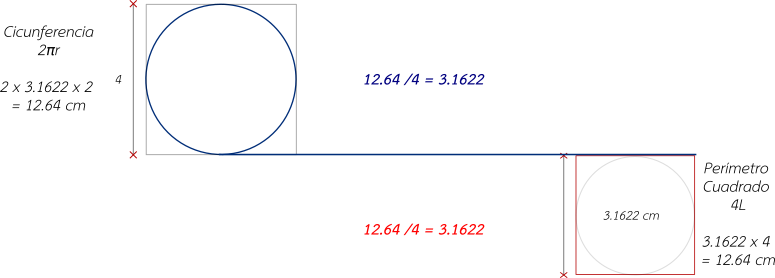
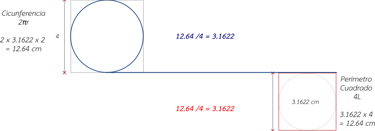
With this present, we start with the circumcircle circumscribed in that quadrilateral, whose circumference gives us the value of: C = 2∏r = 2 x 3.1622 x 2, which is equal to 12.6488 cm. Previously we had also seen how the quadrilateral was formed from a line, in the same way, the solution of the "Quadrature of the Circumference" from another perspective, consists of forming a quadrilateral with the length of the contour of the circumscribed circumference inside the quadrilateral of side 4.
The numerical solution consists of dividing the value of the circumference circumscribed in the quadrilateral of side 4, by 4, that is: 12.6488 cm / 4, which gives us 3.1622 cm, value, which now becomes the value of the side of the quadrilateral, whose perimeter solves the "Quadrature of the Circumference". This process can also be given inversely, which also gives us 3.1622 cm, which represents the fourth part of the value of the circumference, so multiplying this value by 4, gives us the same result of 12.6488 cm, value of the circumference that is equal to the perimeter of the quadrilateral shown.