The Quadrature of the Circle
It is called "Quadrature of the Circle" the unsolvable mathematical problem according to "geometry", which consists in finding -with only ruler and compass- a square that has an area equal to the area of a given circle.
As we have mentioned above, the resolution of this problem was repeatedly tried to be tackled, apparently without success, since ancient times. Speaking in a figured sense, something is said to be the "Square of the Circle" when it represents a very difficult or impossible problem to solve.


The Solution
As we saw in the "Quadrature of the Circumference", the solution to this problem is relatively simple from a certain perspective and very complicated from another, it is easy to find the numerical solution, but it is very complicated to find the detail of how this solution is generated.
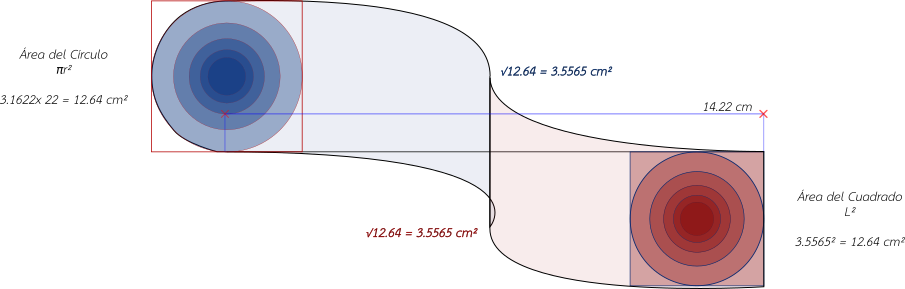
Unlike the "Quadrature of the Circumference" where we had to use the perimeter and the circumference, in the "Quadrature of the Circle" we need to match the area of the circle with the area of the square, which leads us to go from a measurement in centimeters (cm) to a solution in square centimeters (cm²), which is similar to the difference between a line and a plane. In the "Quadrature of the Circumference" we had to match the outline of both the circumference and the quadrilateral, but here we have to match everything inside, that is, the entire interior or area of the circle with the interior or area of the square.
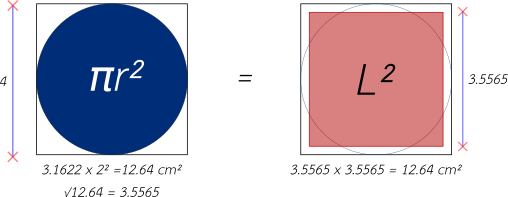
We calculate the value of the area of the circumscribed circle in the square of side 4, a value that gives us: A= r² = 3.1622 x 22 = 12.6488 cm². With this in mind, the numerical solution curiously comes out of taking the "square root" of that same value: √12.6488, which gives us 3.5565 cm, a value that represents the side of the square of 3.5565 x 3.5565 cm, whose area gives us the value of 12.6488 cm² , a value that represents an area equivalent to that of the circumscribed circle inside the square of side 4, an equivalence that allows us to come up with the solution of the "Square of the Circle", which allows us to find the equality between these two "geometric" figures.
In this way, we find numerically a circle and a square whose areas are equivalent. Now, as I said, the numerical solution is simple, what is complicated is how to find how this square is generated, using only "Ruler and Compass", so next we will show a series of methods or possible ways to find this value using numbers and "geometry".